Pythonで円形断面の水深を求める
目的
このプログラムは、円形断面の管路を流れる水の深さや流速、フルード数を計算するためのツールです。水理学的な計算を行うことで、円形断面内の流体の挙動を詳細に解析し、設計や検証の際に役立てることを目的としています。
手法
本プログラムはPythonのライブラリ sympy および tkinter を用いて構築されています。以下にその詳細を示します。
- 数値計算:ニュートン・ラフソン法を用いて中心角(θ)を求め、水深や流積を計算します。
- フルード数の計算:流量、断面積、重力加速度を基にフルード数を計算します。
- GUIの実装:ユーザーが入力しやすいインターフェースを提供し、結果を表形式で表示します。
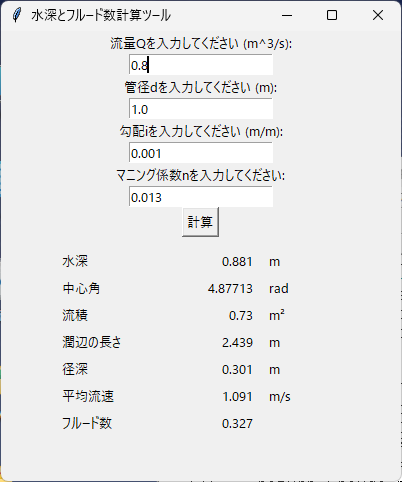
入力例
以下のパラメータを入力として使用します:
- 流量 Q: 0.8 (m³/s)
- 管径 d: 1.0 (m)
- 勾配 i: 0.001 (m/m)
- マニング係数 n: 0.013
出力結果
| 項目 | 値 | 単位 |
|---|---|---|
| 水深 | 0.881 | m |
| 中心角 | 4.87713 | rad |
| 流積 | 0.73 | m² |
| 潤辺の長さ | 2.439 | m |
| 径深 | 0.301 | m |
| 平均流速 | 1.091 | m/s |
| フルード数 | 0.327 |
ソースコード
import sympy as sp
from sympy import sin, cos
from tkinter import *
from tkinter import messagebox
import math
# フルード数を計算する関数
def calculate_froude(Q, A, b, H):
g = 9.81 # 重力加速度 [m/s^2]
V = Q / A # 平均流速 [m/s]
Froude_number = V / math.sqrt(g * (A / b)) # フルード数の計算
return Froude_number, V
# 円形断面での関数を定義
def f(th, i, n, d, Q):
return i**0.5 * (d**2 * (th - sin(th)) / 8) ** (5/3) / n - Q * (d / 2 * th) ** (2/3)
# 変数を定義
th = sp.symbols('th')
def calculate():
try:
# 入力値を取得
Q = float(Q_entry.get())
d = float(d_entry.get())
i = float(i_entry.get())
n = float(n_entry.get())
# 関数とその導関数を定義
f_expr = f(th, i, n, d, Q)
f_expr_diff = sp.diff(f_expr, th)
# 高速計算のためにラムダ関数に変換
f_lambdified = sp.lambdify(th, f_expr, "numpy")
f_diff_lambdified = sp.lambdify(th, f_expr_diff, "numpy")
# 初期値を設定
th_guess = 3.14
# 収束条件の設定
eps = 1.0e-5
# ニュートン・ラフソン法で近似解を求める
prev_th_guess = float('inf')
iterations = 0
max_iterations = 100
while abs(prev_th_guess - th_guess) > eps and iterations < max_iterations: prev_th_guess = th_guess th_guess = th_guess - f_lambdified(th_guess) / f_diff_lambdified(th_guess) iterations += 1 # 収束しなかった場合のエラーハンドリング if iterations >= max_iterations or math.isnan(th_guess):
messagebox.showwarning("計算エラー", "計算が収束しませんでした。流量が大きすぎる可能性があります。")
return
# thから水深Hを求める
H = d / 2 - d / 2 * cos(th_guess / 2)
# 流体の断面積Aを計算
A = (d**2 * (th_guess - sin(th_guess))) / 8
# 水面幅bを計算(円形断面の場合、b = d * sin(th/2))
b = d * sin(th_guess / 2)
# 潤辺の長さPを計算
P = d * th_guess / 2
# 径深Rを計算
R = A / P
# フルード数と平均流速を計算
froude_number, V = calculate_froude(Q, A, b, H)
# 結果フレームをクリアして再表示
for widget in result_frame.winfo_children():
widget.destroy()
# テーブル形式で結果を表示
items = [
("水深", f"{H:.3f}", "m"),
("中心角", f"{th_guess:.5f}", "rad"),
("流積", f"{A:.2f}", "m²"),
("潤辺の長さ", f"{P:.3f}", "m"),
("径深", f"{R:.3f}", "m"),
("平均流速", f"{V:.3f}", "m/s"),
("フルード数", f"{froude_number:.3f}", "")
]
for i, (label_text, value_text, unit_text) in enumerate(items):
Label(result_frame, text=label_text, width=15, anchor="w").grid(row=i, column=0, padx=5, pady=2)
Label(result_frame, text=value_text, width=10, anchor="e").grid(row=i, column=1, padx=5, pady=2)
Label(result_frame, text=unit_text, width=10, anchor="w").grid(row=i, column=2, padx=5, pady=2)
except ValueError:
messagebox.showerror("入力エラー", "無効な入力値があります。数値を入力してください。")
except Exception as e:
messagebox.showerror("エラーが発生しました", f"エラーが発生しました: {e}")
# GUIの作成
root = Tk()
root.title("水深とフルード数計算ツール")
# ウィンドウサイズを設定
root.geometry("400x450")
Q_label = Label(root, text="流量Qを入力してください (m^3/s):")
Q_label.pack()
Q_entry = Entry(root)
Q_entry.pack()
d_label = Label(root, text="管径dを入力してください (m):")
d_label.pack()
d_entry = Entry(root)
d_entry.pack()
i_label = Label(root, text="勾配iを入力してください (m/m):")
i_label.pack()
i_entry = Entry(root)
i_entry.pack()
n_label = Label(root, text="マニング係数nを入力してください:")
n_label.pack()
n_entry = Entry(root)
n_entry.pack()
calculate_button = Button(root, text="計算", command=calculate)
calculate_button.pack()
result_frame = Frame(root)
result_frame.pack(pady=10)
root.mainloop()

コメント