魔方陣とは

魔方陣とは、1から始まる連続する自然数を、各行・各列・対角線の合計がすべて同じになるように配置した正方形のグリッドです。
例えば、3×3の魔方陣では、すべての行、列、対角線の合計が15になります。

魔方陣は、古くからパズルや数学的遊びの一つとして人気があり、古代中国やインドでも見られるパターンの一つです。
特に、奇数サイズの魔方陣は比較的簡単に解くことができ、Siamese法と呼ばれるアルゴリズムが広く用いられています。

解き方
魔方陣Pythonスクリプト

解き方

奇数サイズの魔方陣を解くためには、次のSiamese法を使用します：

1を最初に、最上行の中央に配置します。
次に、右上の隣接セルに移動して、次の数を配置します。
右上がグリッドの外に出た場合は、反対側の端に移動します。
もしすでに数字がある場合、下のセルに移動して配置します。
このプロセスを、すべての数を配置するまで繰り返します。

魔方陣Pythonスクリプト

以下は、Pythonを使用して奇数サイズの魔方陣を生成し、表示するためのスクリプトです。
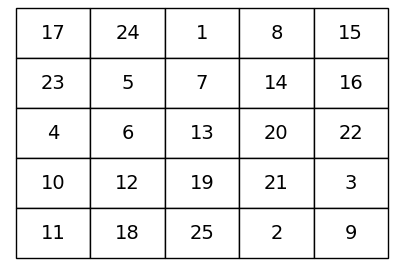
例えば、5×5の魔方陣が生成されます。


import matplotlib.pyplot as plt
import numpy as np

def generate_magic_square(n):
    if n % 2 == 0:
        raise ValueError("N must be an odd number")
    
    magic_square = [[0] * n for _ in range(n)]
    
    row = 0
    col = n // 2
    
    for num in range(1, n * n + 1):
        magic_square[row][col] = num

        new_row = (row - 1) % n
        new_col = (col + 1) % n

        if magic_square[new_row][new_col] != 0:
            row = (row + 1) % n
        else:
            row = new_row
            col = new_col

    return magic_square

def plot_magic_square(magic_square):
    n = len(magic_square)
    
    fig, ax = plt.subplots()
    ax.set_axis_off()
    
    table_data = np.array(magic_square)
    
    # 表の描画
    table = ax.table(cellText=table_data, loc='center', cellLoc='center', colWidths=[0.1] * n)
    
    # フォントサイズやセルのスタイル設定
    table.auto_set_font_size(False)
    table.set_fontsize(14)
    table.scale(1.5, 3)
    
    plt.show()

# N×Nの魔法陣を作成
N = 5
magic_square = generate_magic_square(N)
plot_magic_square(magic_square)

このスクリプトを実行すると、指定したサイズの魔方陣が描画されます。
今回は5×5の魔方陣を例として使用していますが、他の奇数サイズでも動作します。
#魔法陣 #Python