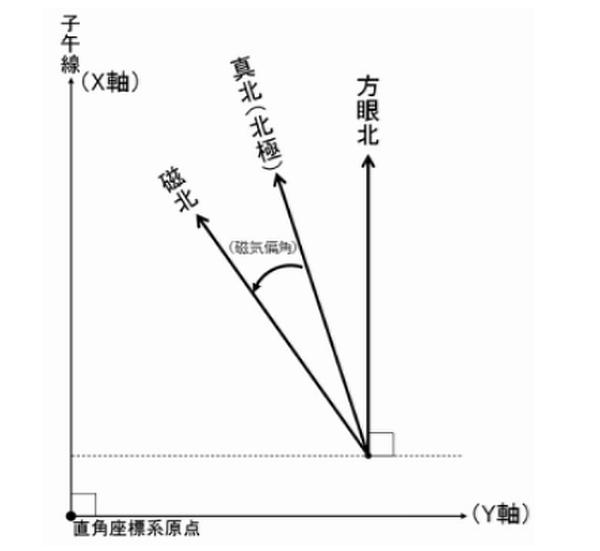
磁気偏角について

磁気偏角とは、コンパスが指す「磁北」と、地図上の「真北」との間の角度差を指します。これにより、磁気コンパスを使用する際には、真北との誤差を補正する必要があります。

磁気偏角の特徴
磁場要素の説明
偏角と磁場要素の計算方法
計算結果
計算結果の利用
関連リンク

磁気偏角の特徴

地球の磁場により、地域ごとに異なる。
西偏角：磁北が真北の西側にある場合（正の値）。
東偏角：磁北が真北の東側にある場合（負の値）。
定期的な測定が必要：地球の磁場は常に変動しているため、定期的な観測が求められます。
偏角の影響は、特に航海や航空でのナビゲーションにおいて重要。

磁場要素の説明

磁場要素には、以下の5つが含まれます。これらの要素は、地球の磁場に関連する様々な情報を提供し、航海、航空、地質学など多くの分野で役立ちます。

1. 偏角 (D2020.0)

偏角とは、磁北（コンパスが指す北）と真北（地図上の北）の間の角度差です。偏角が大きい地域では、コンパスによる方位確認の際に誤差を補正する必要があります。

2. 伏角 (I2020.0)

伏角とは、磁場の水平面に対する鉛直成分の角度です。伏角が大きいほど、磁場が地面に対して垂直に強く作用していることを意味します。

3. 全磁力 (F2020.0)

全磁力とは、地磁気の全体の強さを示します。単位はナノテスラ（nT）で、全磁力が大きいほど磁場が強いことを示しています。

4. 水平分力 (H2020.0)

水平分力とは、地磁気の水平方向の成分を示し、コンパスが正しく機能するために重要です。水平分力が小さいと、コンパスの指針が安定しないことがあります。

5. 鉛直分力 (Z2020.0)

鉛直分力とは、地磁気の鉛直方向の成分です。これは、鉱物探査や地質学的な調査で役立つ重要な情報を提供します。

偏角と磁場要素の計算方法

以下のPythonスクリプトを使用すると、任意の地点における偏角や磁場要素（伏角、全磁力、水平分力、鉛直分力）を簡単に計算することができます。


import math

def calculate_magnetic_elements(lat, lon):
    # 緯度・経度の差分を計算
    delta_phi = lat - 37  # Δφ = φ - 37°
    delta_lambda = lon - 138  # Δλ = λ - 138°

    # 偏角 (D2020.0) の計算 (単位: 分)
    D = (8 * 60 + 15.822) + 18.462 * delta_phi - 7.726 * delta_lambda + 0.007 * (delta_phi ** 2) - 0.007 * delta_phi * delta_lambda - 0.655 * (delta_lambda ** 2)
    D_deg = int(D // 60)
    D_min = D % 60

    # 伏角 (I2020.0) の計算 (単位: 分)
    I = (51 * 60 + 26.559) + 72.683 * delta_phi - 8.642 * delta_lambda - 0.943 * (delta_phi ** 2) - 0.142 * delta_phi * delta_lambda + 0.585 * (delta_lambda ** 2)
    I_deg = int(I // 60)
    I_min = I % 60

    # 全磁力 (F2020.0) の計算 (単位: nT)
    F = 47881.463 + 547.650 * delta_phi - 256.043 * delta_lambda - 2.388 * (delta_phi ** 2) - 2.750 * delta_phi * delta_lambda + 5.199 * (delta_lambda ** 2)

    # 水平分力 (H2020.0) の計算 (単位: nT)
    H = 29855.926 - 439.613 * delta_phi - 74.293 * delta_lambda - 6.703 * (delta_phi ** 2) + 7.987 * delta_phi * delta_lambda - 5.094 * (delta_lambda ** 2)

    # 鉛直分力 (Z2020.0) の計算 (単位: nT)
    Z = 37441.791 + 1058.480 * delta_phi - 274.371 * delta_lambda - 10.853 * (delta_phi ** 2) - 6.454 * delta_phi * delta_lambda + 9.899 * (delta_lambda ** 2)

    # 結果を出力
    print(f"緯度: {lat}°, 経度: {lon}°")
    print(f"偏角 (D2020.0): {D_deg}°{D_min:.3f}′")
    print(f"伏角 (I2020.0): {I_deg}°{I_min:.3f}′")
    print(f"全磁力 (F2020.0): {F:.3f} nT")
    print(f"水平分力 (H2020.0): {H:.3f} nT")
    print(f"鉛直分力 (Z2020.0): {Z:.3f} nT")

# 使用例: 東京（北緯 35.68°, 東経 139.70°）
calculate_magnetic_elements(35.68, 139.70)

計算結果

上記のスクリプトを実行すると、東京（緯度 35.68°, 経度 139.70°）における磁場要素は以下の通りになります。

偏角 (D2020.0): 7°36.500′
伏角 (I2020.0): 50°34.053′
全磁力 (F2020.0): 47833.175 nT
水平分力 (H2020.0): 29837.683 nT
鉛直分力 (Z2020.0): 37413.812 nT

計算結果の利用

上記のスクリプトを使用すると、任意の地点における磁気偏角や伏角などの磁場要素を計算できます。
航海や航空でのナビゲーションにおいて、コンパスの誤差を補正するために利用されます。
地図やGPSの「真北」とコンパスの「磁北」の間に存在する角度差を知ることができます。
地質学的調査や鉱物探査においても、磁場要素は有用です。
地質学的調査や鉱物探査においても、磁場要素は有用です。特に鉛直分力や伏角は、地下の構造を把握するための重要な手がかりを提供します。
太陽活動によって発生する磁気嵐の影響をモニタリングするためにも、全磁力の情報は重要です。通信や電子機器に影響を与える磁場の変動を監視するのに役立ちます。